Jak podzielić tort?

Mieszkam i  pracuję w  New Haven w  stanie Connecticut. Miasto to słynie, oprócz Uniwersytetu Yale, z  pizzy. Niektórzy są zagorzałymi i lojalnymi wielbicielami restauracji Sally’s, a inni Pepe. Widząc długie kolejki, można pomyśleć, że trudniej się do nich dostać niż na  Yale. To dlatego, że ich pizza z  małżami jest klasą samą w sobie. Ryzykując przyznanie racji którejś ze stron, obserwuję negocjacje nad pizzą od Pepe.

Alice i  Bob dostaną od Pepe pizzę z małżami pokrojoną na 12 kawałków, jeśli dojdą do porozumienia, jak ją podzielić między siebie. Jeśli się nie dogadają, to dostaną od Pepe pizzę, ale tylko jej połowę, z  podziałem preferencyjnym: cztery kawałki trafią do Alice, a  dwa do Boba.

Jest wiele zachęt, aby dojść do porozumienia. Problem polega na  tym, że jest wiele rozwiązań korzystnych dla każdej ze stron, ale jedne są lepsze dla Alice, a  inne dla Boba. Muszą wybrać jedno. Większość ludzi przyjmuje jedną z dwóch perspektyw co do tego, jak Alice i  Bob mogą negocjować porozumienie.

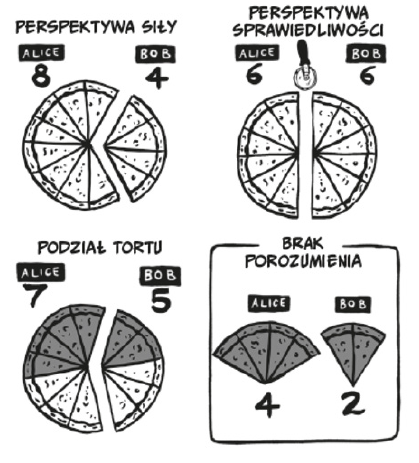
Pierwsza perspektywa to perspektywa siły. Alice zaczyna z większą siłą – powinna dostać dwa razy więcej: osiem kawałków dla Alice i  cztery dla Boba.

Druga perspektywa to perspektywa sprawiedliwości. Obie strony skupiają się na  tym, co ostatecznie dostaną. W  tym scenariuszu dzielą pizzę na  połowę: Alice dostaje sześć kawałków i Bob dostaje sześć kawałków.

Jest jeszcze inny – i  bardziej logiczny – sposób podziału pizzy. Skupia się na  tym, o  co tak naprawdę chodzi w  negocjacjach: o  dodatkowe sześć kawałków zdobyte dzięki dojściu do porozumienia. Jeśli Alice i  Bob się nie dogadają, to będą mieć łącznie 6 kawałków (4 + 2). Jeśli osiągną porozumienie, będą mieć łącznie 12 kawałków. Wartością dodaną dojścia do porozumienia jest zwiększenie liczby otrzymanych wspólnie kawałków z  sześciu do dwunastu. To jest właśnie ta stawka, czyli to, co nazywam tortem negocjacyjnym. Aby uzyskać te sześć dodatkowych kawałków, potrzebne jest takie samo zaangażowanie Alice i  Boba. Ponieważ ich siła jest równa, sześć kawałków powinno zostać podzielone po równo. Oprócz tego w przypadku niedojścia do porozumienia każda ze stron otrzymuje swoją sumę gwarantowaną. To prowadzi ostatecznie do takiego podziału: 4 + 3 = 7 kawałków dla Alice i 2 + 3 = 5 kawałków dla Boba.

Choć może to zabrzmieć dziwnie, większość ludzi gubi się w  końcu w  tym, o  co tak naprawdę toczą się negocjacje. Spierają się raczej o  dwanaście kawałków, a nie o sześć. Skupiają się na całej pizzy, a nie na istotnej części negocjacji. Tort negocjacyjny wydaje się oczywisty i w zasięgu wzroku. Gdy spojrzysz na negocjacje w kategoriach istotnej części tortu, logiczny wydaje się wniosek, że ta istotna część powinna zostać podzielona równo. To właśnie do tego powinienem cię przekonać. Potem dam ci narzędzia do przekonywania innych.

W pierwszym kroku chcę wyjaśnić, co jest nie tak ze status quo. W mojej opinii perspektywa siły myli władzę posiadaną poza negocjacjami z siłą w negocjacjach. Dlaczego łączna liczba powinna zostać podzielona proporcjonalnie do liczby opcji na wypadek niedojścia do porozumienia? Kawałki pizzy nie negocjują ze sobą – Alice i Bob tak. Podczas gdy podział w stosunku 8:4 wydaje się rozsądnym rozwiązaniem, ponieważ odzwierciedla proporcję ilości gwarantowanej w  razie braku porozumienia, nie ma żadnego powodu, aby ostatecznie podzielić całość w  takiej proporcji.

Ktoś może twierdzić, że Bob jest na słabszej pozycji przetargowej, ponieważ w  sytuacji braku porozumienia otrzyma tylko dwa kawałki. Alice dostanie cztery. Ten argument rozmija się jednak z  celem negocjacji. Jeśli Alice i  Bob nie osiągną porozumienia, Alice nie dostanie nic więcej oprócz czterech kawałków, tak samo jak Bob – on nie dostanie nic więcej oprócz dwóch kawałków. W  skutecznych negocjacjach chodzi o  to, aby wyjść z  sytuacji braku porozumienia. W  przypadku Alice i Boba każde z  nich jest tak samo potrzebne do osiągnięcia porozumienia, zatem ich siła jest jednakowa.

Drugie podejście, równy podział całości, jest zbyt uproszczonym pojmowaniem sprawiedliwości. W  sytuacji, w której dzielimy dwanaście kawałków, Alice i Bob nie są na tych samych pozycjach. Alice ma większą wartość gwarantowaną na  wypadek braku porozumienia. Gdyby podział 6:6 był naprawdę sensownym odzwierciedleniem sprawiedliwości, powinien obowiązywać w  każdym przypadku braku porozumienia. A  nie obowiązuje. Popatrzmy, co się stanie, gdy liczba gwarantowana Alice w przypadku braku porozumienia wzrośnie do siedmiu kawałków, a  dla Boba pozostaną dwa. Jeśli sprawiedliwość oznacza podział 6:6, Alice odrzuci taką propozycję. Będzie wolała zatrzymać swoje gwarantowane siedem kawałków niż przyjąć sześć. Wprawdzie ta wada równego podziału może nie być oczywista, gdy ilości gwarantowane na wypadek braku porozumienia wynoszą cztery i dwa, jednak widzimy, że przyjęcie jako zasady sprawiedliwości podziału całości na dwa jest fundamentalnie wadliwe.